本篇主要内容:递归以及冒泡排序
参考文章:(http://www.cnblogs.com/balian/archive/2011/02/11/1951054.html)
递归的概念
递归的概念很简单,如果函数包含了对其自身的调用,该函数就是递归的。或者说:如果一个新的调用能在相同过程中较早的调用结束之前开始,那么个该过程就是递归。(《Python核心编程第二版》的第304页)
这里插入一些关于递归的网上解释,因为我是从网上搜到的这些内容:
(1)递归就是在过程或函数里调用自身;(2)在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。递归算法一般用于解决三类问题:
(1)数据的定义是按递归定义的。(比如Fibonacci函数)(2)问题解法按递归算法实现。(回溯)(3)数据的结构形式是按递归定义的。(比如树的遍历,图的搜索)递归的缺点:递归算法解题的运行效率较低。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。
递归程序的基本步骤,来自()
每一个递归程序都遵循相同的基本步骤:
1.初始化算法。递归程序通常需要一个开始时使用的种子值(seed value)。要完成此任务,可以向函数传递参数,或者提供一个入口函数,这个函数是非递归的,但可以为递归计算设置种子值。 2.检查要处理的当前值是否已经与基线条件相匹配(base case)。如果匹配,则进行处理并返回值。 3.使用更小的或更简单的子问题(或多个子问题)来重新定义答案。 4.对子问题运行算法。 5.将结果合并入答案的表达式。 6.返回结果。基线条件(base case)。基线条件是递归程序的最底层位置,在此位置时没有必要再进行操作,可以直接返回一个结果。所有递归程序都必须至少拥有一个基线条件,而且必须确保它们最终会达到某个基线条件;否则,程序将永远运行下去,直到程序缺少内存或者栈空间。
自己总结了一下,要写一个递归的程序,需要这样做:
1.一个基线条件。请在递归函数的一开始就处理这个基线条件。2.一系列的规则,使对递归函数的每次调用都趋进于直至达到这个基线条件。
递归的例子
对列表[33,2,10,1]进行冒泡排序
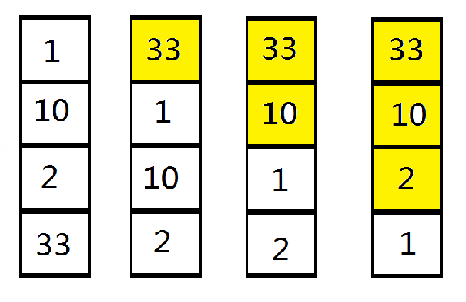
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个(已经比较出的最大数)。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
li = [33,2,10,1]for i in range(1, len(li)): for j in range(len(li) - i): if li[j] > li[j + 1]: li[j], li[j + 1] = li[j + 1], li[j]print(li)
用递归实现的非波拉契数列
def f5(depth, a1, a2): # 定义层数到了,则return if depth == 10: return a1 a3 = a1 + a2 r = f5(depth + 1,a2, a3) return rret = f5(1, 0, 1)print(ret)
生成包含数字字母的随机验证码例子
import randomtemp = ""for i in range(6): num = random.randrange(0,4) if num == 3 or num == 1: rad1 = random.randrange(1,11) temp += str(rad1) else: rad2 = random.randrange(65,91) c2 = chr(rad2) temp += c2print(temp)